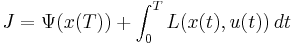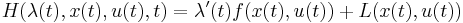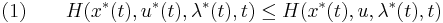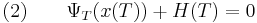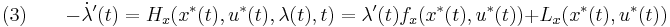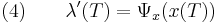Pontryagin's minimum principle
Pontryagin's maximum (or minimum) principle is used in optimal control theory to find the best possible control for taking a dynamical system from one state to another, especially in the presence of constraints for the state or input controls. It was formulated in 1956 by the Russian mathematician Lev Semenovich Pontryagin and his students. It has as a special case the Euler–Lagrange equation of the calculus of variations.
The principle states informally that the Hamiltonian must be minimized over 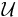 , the set of all permissible controls. If
, the set of all permissible controls. If 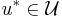 is the optimal control for the problem, then the principle states that:
is the optimal control for the problem, then the principle states that:
where ![x^*\in C^1[t_0,t_f]](/2012-wikipedia_en_all_nopic_01_2012/I/61d8ab972702f3b4723a61a755d7407f.png) is the optimal state trajectory and
is the optimal state trajectory and ![\lambda^* \in BV[t_0,t_f]](/2012-wikipedia_en_all_nopic_01_2012/I/27b8b76939dc098d8ec6bc8f2d040375.png) is the optimal costate trajectory.
is the optimal costate trajectory.
The result was first successfully applied into minimum time problems where the input control is constrained, but it can also be useful in studying state-constrained problems.
Special conditions for the Hamiltonian can also be derived. When the final time 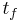 is fixed and the Hamiltonian does not depend explicitly on time
is fixed and the Hamiltonian does not depend explicitly on time 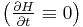 , then:
, then:
and if the final time is free, then:
More general conditions on the optimal control are given below.
When satisfied along a trajectory, Pontryagin's minimum principle is a necessary condition for an optimum. The Hamilton–Jacobi–Bellman equation provides sufficient conditions for an optimum, but this condition must be satisfied over the whole of the state space.
Contents |
Maximization and minimization
The principle was first known as Pontryagin's maximum principle and its proof is historically based on maximizing the Hamiltonian. The initial application of this principle was to the maximization of the terminal velocity of a rocket. However as it was subsequently mostly used for minimization of a performance index it is also referred to as the minimum principle. Pontryagin's book solved the problem of minimizing a performance index.[1]
Notation
In what follows we will be making use of the following notation.
Formal statement of necessary conditions for minimization problem
Here the necessary conditions are shown for minimization of a functional. Take  to be the state of the dynamical system with input
to be the state of the dynamical system with input  , such that
, such that
where 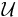 is the set of admissible controls and
is the set of admissible controls and  is the terminal (i.e., final) time of the system. The control
is the terminal (i.e., final) time of the system. The control 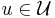 must be chosen for all
must be chosen for all ![t \in [0,T]](/2012-wikipedia_en_all_nopic_01_2012/I/e66a2b7fedcba80ccb192b87440f8d9c.png) to minimize the objective functional
to minimize the objective functional 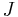 which is defined by the application and can be abstracted as
which is defined by the application and can be abstracted as
The constraints on the system dynamics can be adjoined to the Lagrangian  by introducing time-varying Lagrange multiplier vector
by introducing time-varying Lagrange multiplier vector  , whose elements are called the costates of the system. This motivates the construction of the Hamiltonian
, whose elements are called the costates of the system. This motivates the construction of the Hamiltonian  defined for all
defined for all ![t \in [0,T]](/2012-wikipedia_en_all_nopic_01_2012/I/e66a2b7fedcba80ccb192b87440f8d9c.png) by:
by:
where 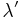 is the transpose of
is the transpose of  .
.
Pontryagin's minimum principle states that the optimal state trajectory 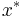 , optimal control
, optimal control 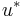 , and corresponding Lagrange multiplier vector
, and corresponding Lagrange multiplier vector 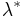 must minimize the Hamiltonian
must minimize the Hamiltonian  so that
so that
for all time ![t \in [0,T]](/2012-wikipedia_en_all_nopic_01_2012/I/e66a2b7fedcba80ccb192b87440f8d9c.png) and for all permissible control inputs
and for all permissible control inputs 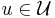 . It must also be the case that
. It must also be the case that
Additionally, the costate equations
must be satisfied. If the final state 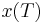 is not fixed (i.e., its differential variation is not zero), it must also be that the terminal costates are such that
is not fixed (i.e., its differential variation is not zero), it must also be that the terminal costates are such that
These four conditions in (1)-(4) are the necessary conditions for an optimal control. Note that (4) only applies when 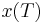 is free. If it is fixed, then this condition is not necessary for an optimum.
is free. If it is fixed, then this condition is not necessary for an optimum.
See also
- Lagrange multipliers on Banach spaces, Lagrangian method in calculus of variations
Notes
- ^ L. S. Pontryagin, V. G. Boltyanskii, R. V. Gamkrelidze, E. F. Mishchenko, The Mathematical Theory of Optimal Processes, page 19, vol. 4. Interscience, 1962. Translation of a Russian book. ISBN 2881240771 and ISBN 978-2881240775
References
- Pontryagin, L.S. et al. The Mathematical Theory of Optimal Processes, vol. 4. Interscience, 1962. Translation of a Russian book. ISBN 2881240771 and ISBN 978-2881240775
- Fuller A.T. Bibliography of Pontryagin's maximum principle, J. Electronics & Control vol.15 no.5 Nov. 1963 pp. 513–517
- Kirk, D.E. Optimal Control Theory, An Introduction, Prentice Hall, 1970. ISBN 0486434842
- Sethi, S. P. and Thompson, G. L. Optimal Control Theory: Applications to Management Science and Economics, 2nd edition, Springer, 2000. ISBN 0387280928 and ISBN 0792386086. Slides are available at http://www.utdallas.edu/~sethi/OPRE7320presentation.html
- Geering, H.P. Optimal Control with Engineering Applications, Springer, 2007. ISBN 978-3-540-69437-3
- Ross, I. M. A Primer on Pontryagin's Principle in Optimal Control, Collegiate Publishers, 2009. ISBN 978-0-9843571-0-9. (http://www.ElissarGlobal.com free chapter on Pontryagin's Principle).
![H(x^*(t),u^*(t),\lambda^*(t),t) \leq H(x^*(t),u,\lambda^*(t),t), \quad \forall u \in \mathcal{U}, \quad t \in [t_0, t_f]](/2012-wikipedia_en_all_nopic_01_2012/I/5885dcaca3bd4f03d638e66637dcf860.png)
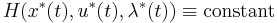
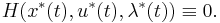
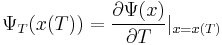
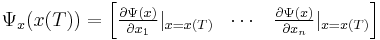
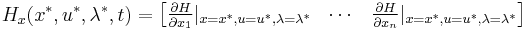
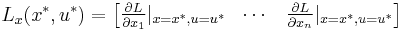
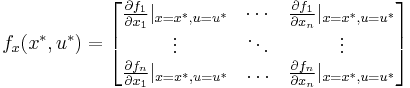
![\dot{x}=f(x,u), \quad x(0)=x_0, \quad u(t) \in \mathcal{U}, \quad t \in
[0,T]](/2012-wikipedia_en_all_nopic_01_2012/I/39aa7ef71eaad4c077dec52829697fb1.png)